Centre of gravity and T-section problem - Engineering Mechanics

               

                    CENTRE OF GRAVITY

So 1^st of all in these articles we know about the centre of gravity and centroid. It’s a very important and basic chapter or topic in Engineering Mechanics. But one thing I clear to all, the centre of gravity is not a very easy chapter because various type mathematical problems you will face. But there is nothing to fear, I’ll try to make it easier for you to understand. So read the article completely and then comment below for any problem regarding this article.

So, Let’s Start –

What is Centroid?

In our world, the plane figures like a triangle, quadrilateral, circle etc. have the only area, but no mass. The centre of the area of such figures is known as centroid.

 Also Read- factors-controlling-alignment.

What is the Centre of gravity?

In one sentence, the Centre of gravity is the point which resultant gravitational force (weight) acts for any the orientation of the body.

 

If I tell to break it, then it’s a point have all elements in the world. The centre of gravity is the average location of the weight of an object. Centre of gravity is above its base of support will be stable only as long the vertical line downward from the centre of gravity falls within the base of support. The critical point is reached when the centre of gravity is no longer above the base of support.

 Also Read:-indian-road-development-plan-nagpur.

 

The centre of gravity of some simple figures are given below –

 

1) The centre of gravity of a uniform rod is its middle point.

 

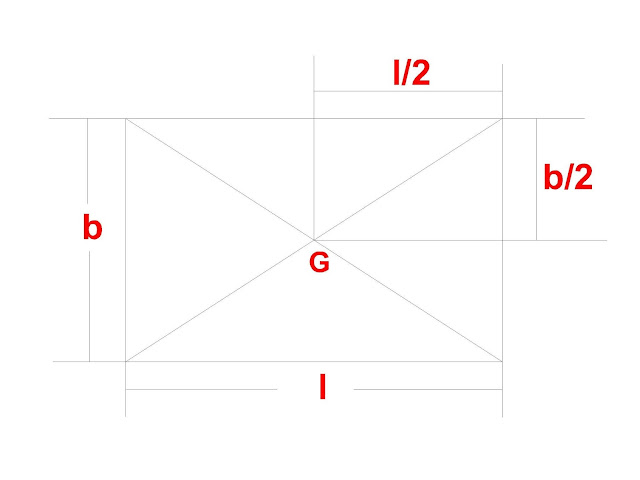
2) The centre of gravity of rectangular (or parallelogram) lies at a point where its diagonals intersect.

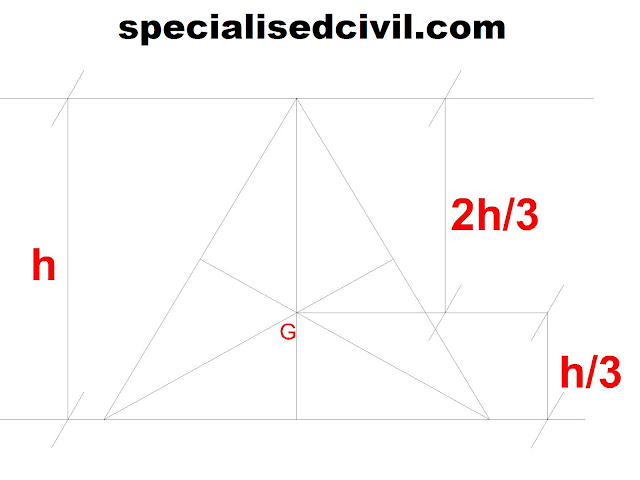
3) The centre of gravity of a triangle lies at a point where the three medians of the triangle intersect.

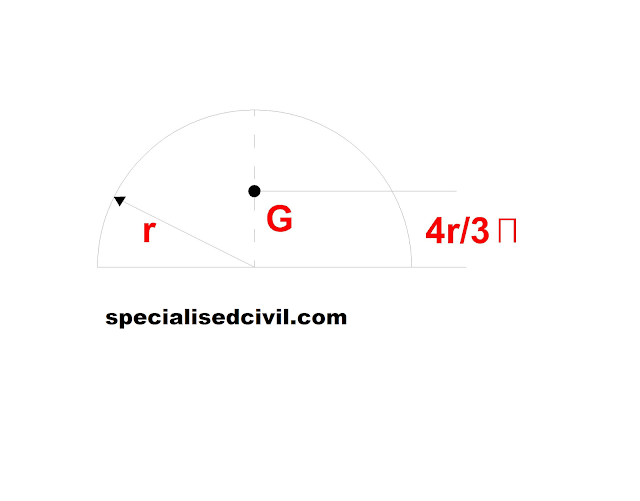
4) The centre of gravity of a semi-circle lies at a distance of 4r/3Π from its base measured along the vertical radius.

5) The centre of gravity of a hemisphere lies at a distance of 3r/8 from its base, measured along the vertical radius.

 

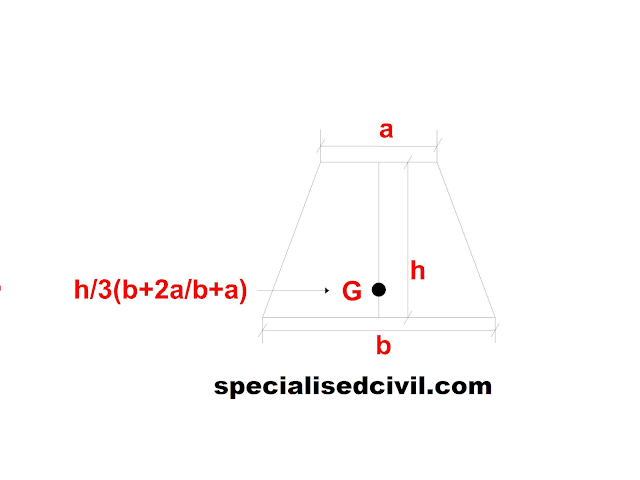
6) The centre of gravity of a trapezium with parallel sides a & b lies at a distance of   ) measured from side b.

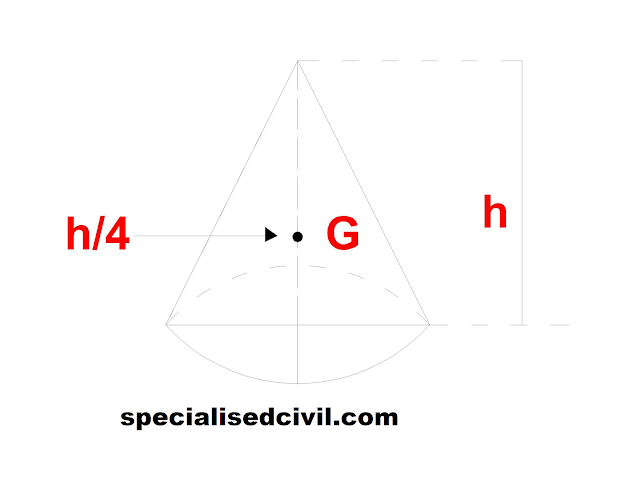
7) The centre of gravity of a right circular solid cone lies at a distance of h/4 from its base, measured along the vertical axis.

 Also Read:-how-do-we-test-quality-of-cement-at.

Find the centre of gravity of a 100×150×30mm T-section.

As the section is symmetrical about Y-Y axis, bisecting the web, therefore its CG will lie on this axis. Split up the section two rectangles,

ABCH and DEFG are two rectangles, in figure

Let the bottom of the flange FE be the axis reference,

1^st step,

Area of ABCH rectangle,

 

A₁ = 100×30 = 3000 mm²

 

Y₁ = (150 – ) = 135mm

 

2^nd step,

Area of DEFE rectangle,

 

A₂ = 120×30 = 3600mm²

 

Y₂ =  = 60mm

We know that distance between CG of the section and bottom of the flange FE,

 

yˉ = 94.1mm